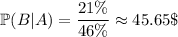Question

In the United States, 46% of all children get an allowance and 21% of all children get an allowance and do household chores. What is the probability that a child does household chores given that the child gets an allowance? I'd appreciate it if you could explain how you got your answer.

Answer 1

Let
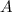
`A` denote the event that a child has an allowance, and
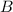
`B` that a child does chores.

The definition of conditional probability says that


`\mathbb P(B|A)=(\mathbb P(B\cap A))/(\mathbb P(A))`

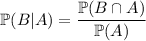
Assuming the events are independent, you could expand the numerator as
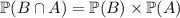
`\mathbb P(B\cap A)=\mathbb P(B)*\mathbb P(A)`. Otherwise, you would need to know that exact probability.

You're given that
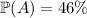
`\mathbb P(A)=46\%`, while
`\mathbb P(B\cap A)=21\%`.

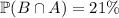
So, the desired conditional probability is


`\mathbb P(B|A)=(21\%)/(46\%)\approx45.65\$`