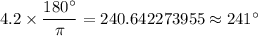Question

If the arc length of a sector in the unit circle is 4.2, what is the measure of the angle of the sector?

Answer 1

The unit circle is a circle with radius
`r=1`, so you have


`L=r\theta\implies4.2=\theta`

where
`\theta` is measured in radians, so
`\theta\approx241^\circ`.

Answer 2

Answer: 4.2 radian or
`241^(\circ)`

Explanation:

Let
`\theta` represents the measure of the angle of the sector.

We know that in a unit circle , the radius = 1 unit

The formula to calculate the length of arc of sector is given by :-

`L=r\theta`

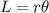
Then , the measure of the angle of the sector is given by :-

`\theta=(L)/(r)\\\\\Rightarrow\ \theta=(4.2)/(1)=4.2\text{ radian}`

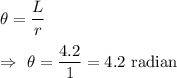
In degrees , the measure of the angle of the sector will be :-

`4.2*(180^(\circ))/(\pi)=240.642273955\approx241^(\circ)`