Answer:
The length of rope is 20.0 ft . Hence, option (1) is correct.
Explanation:
In the figure below AB represents pole having height 10 ft and AC represents the rope that is from the top of pole to the ground. BC represent the ground distance from base of tower to the rope.
The rope and the ground form a 30 degree angle that is the angle between BC and AC is 30°.
In right angled triangle ABC with right angle at B.
Since we have to find the length of rope that is the value of side AC.
Using trigonometric ratios
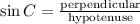
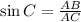
Putting values,
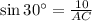
We know,

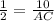
On solving we get,
AC= 20.0 ft
Thus, the length of rope is 20.0 ft
Hence, option (1) is correct.