1. N is a midpoint of the segment KL, then N has coordinates
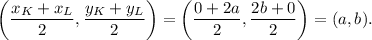
2. To find the area of △KNM, the length of the base MK is 2b, and the length of the height is a. So an expression for the area of △KNM is
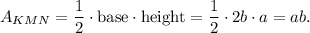
3. To find the area of △MNL, the length of the base ML is 2a and the length of the height is b. So an expression for the area of △MNL is
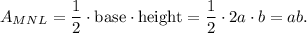
4. Comparing the expressions for the areas you have that the area
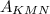 is equal to the area
is equal to the area
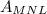 . This means that the segment from the midpoint of the hypotenuse of a right triangle to the opposite vertex forms two triangles with equal areas.
. This means that the segment from the midpoint of the hypotenuse of a right triangle to the opposite vertex forms two triangles with equal areas.