Question

Which represents the solution(s) of the system of equations, y = –x2 + 6x + 16 and y = –4x + 37? Determine the solution set algebraically.

a.(3, 25)
b.(–3, 49)
c.(3, 25) and (7, 9)
d.(–3, 49) and (–7, 65)

Answer 1

TO determine the solution set of the equations given above, we can use substitution method. We do as follows:

y = –x2 + 6x + 16 and y = –4x + 37

–x2 + 6x + 16 = –4x + 37
-x^2 +10x -21 = 0
x = 7 and 3
y = 9 and 25

Therefore, option C is the correct answer.

Answer 2

Answer: c.(3, 25) and (7, 9)

y = –x^2 + 6x + 16 and y = –4x + 37

Plug in -4x+37 for y in first equation . It becomes

`-x^2 + 6x + 16= -4x+37`

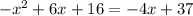
Combine like terms. add 4x and subtract 37 on both sides

`-x^2 + 10x - 21=0`

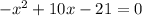
Divide the whole equation by -1 to remove negative sign from -x^2

`x^2 - 10x + 21=0`

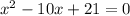
Now factor the left hand side

(x-7)(x-3) = 0

x-7 =0 and x-3=0

x= 7 and x=3

Now we find out y using y = –4x + 37

when x= 7 , then y=-4(7) +37 = 9

when x= 3, then y=-4(3) + 37 = 25

We write solution set as (x,y)

(7,9) and (3,25) is our solution set