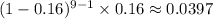Question

If the probability of success during a single event of a geometric experiance is 0.16 what is the probability of success by the 9th event

Answer 1

For a geometric experiment involving
`n` trials and an event that occurs with probability
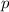
`p`, the probability that the event of interest will occur in the first trial is
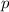
`p`. If it fails in the first trial but succeeds in the second, the probability of this occurring would be
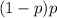
`(1-p)p`. If the first two trials fail but the third succeeds, the probability of this happening is
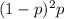
`(1-p)^2p`. And so on.

The unfolding pattern suggests that the probability of success in the
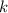
`k`th trial is
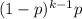
`(1-p)^(k-1)p`, where
`1\le k\le n`.

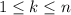
This means the probability of this event happening by the 9th trial is


`(1-0.16)^(9-1)*0.16\approx0.0397`