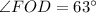Answer:
Option B is correct,
The value of
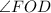 is
is
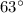
Step-by-step explanation:
From the given figure;
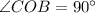 ,
,
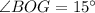 , and
, and
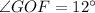 .
.
Linear pair is a pair of adjacent angles formed when two lines intersect. i.e,
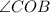 and
and
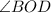 are linear pairs.
are linear pairs.
Also, the two angles of linear pair are always supplementary angle[ measure of a straight angle is 180 degrees].
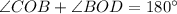
we can write
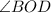 as
as
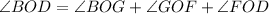
then;
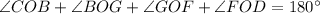
Substitute the given values above to solve for angle FOD;
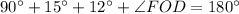
or
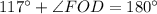
Simplify:
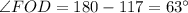
Therefore, the value of