I would say yes.
Typically synthetic division is taught to make it seem like the algorithm only works for rational functions of the form
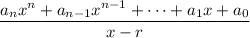
, i.e. only when the divisor

is a monic linear polynomial.
However there are expanded algorithms that would allow for division of something like
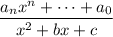
(dividing by higher order monic polynomials) as well as
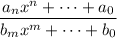
(dividing by any higher order polynomial provided that

).
Consult the Wiki page on "synthetic division" for more info.