Answer:

Explanation:
Standard form of equation of line =
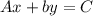 , where A= positive integer and B and C are integers.
, where A= positive integer and B and C are integers.
The equation of a line that passes through two points (a,b) and (c,d) is given by :-
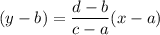
Then, the equation of a line that passes through (1, 5) and (-2, 3) will be :-
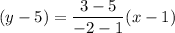
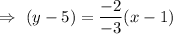
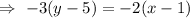

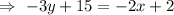 [∵ (-)(-)=(+)]
[∵ (-)(-)=(+)]
 [Add 2x on both sides and subtract 15 on sides.]
[Add 2x on both sides and subtract 15 on sides.]
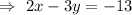
Hence, the standard form of the line that passes through (1, 5) and (-2, 3) :
