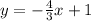a)
The line labelled l1 is a horizontal line.
The equation of the horizontal line is y = b, where b is the point where it intersects the y axis.
Line l1 intersects the y axis at (0,8).
The equation of line l1 is y = 8.
b)
Line l2 passes through (4,1) and (0,-2)
m=Slope of line =
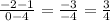
Also -2 is the y intercept.
So b = -2
The equation is
y=mx+b
y=
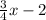
3)
Any line parallel to the given line has the same slope but different y intercept.
So y =
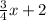
shall be the equation of a line parallel to line l2
d)
For a perpendicular line its slope is -1/m
Slope =
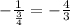
Let the y intercept be 1
The equation of line shall be