Question

Which sum or difference identity would you use to verify that cos (180° - q) = -cos q?

Answer 1

cos (180° - q) = -cos q
First you would use the sum and difference formula of
cos(a – b) = cos(a)cos(b) + sin(a)sin(b) because you have a difference inside the parentheses for cosine.

Hope this helps.

Answer 2

`\cos (a-b)=\cos a \cos b+\sin a \sin b`

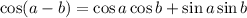
Explanation:

Given :
`\cos (180^(\circ)-q)=-\cos q`

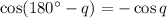
We have to write which identity we will use to prove the given statement.

Consider
`\cos (180^(\circ)-q)=-\cos q`

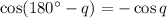
Take left hand side of given expression
`\cos (180^(\circ)-q)`

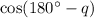
We know

`\cos (a-b)=\cos a \cos b+\sin a \sin b`

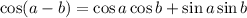
Comparing , we get, a= 180° and b = q

Substitute , we get,

`\cos (180^(\circ)-q)=\cos 180^(\circ)  \cos (q)+\sin q \sin 180^(\circ)`

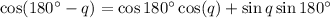
Also, we know
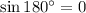`\sin 180^(\circ)=0` and
`\cos 180^(\circ)=-1`

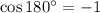
Substitute, we get,

`\cos (180^(\circ)-q)=-1\cdot \cos (q)+\sin q \cdot 0`

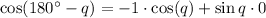
Simplify , we get,

`\cos (180^(\circ)-q)=-\cos (q)`

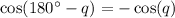
Hence, use difference identity to prove the given result.