Question

Tell whether the lines for each pair of equations are parallel, perpendicular, or neither

y= -3x + 7 -2x+6y=3

Answer 1

6y = -x - 7
y= 6x - 3
__________________

y = x/6 + 7/6
y= 6x - 3

Compare the gradients, one is 1/6, one is 6. These are not parallel because they aren't the same, and not perpendicular because they aren't negative reciprocals. Therefore, neither.

Answer 2

Answer:

Perpendicular lines

Explanation:

We are given that

`y=-3x+7`

`-2x+6y=3`

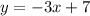
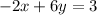
We have to find the pair of equations are parallel , perpendicular or neither.

Differentiate each equation w.r.t.x

`m_1=(dy)/(dx)=-3`

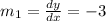
Using rule :
`(dx^n)/(dx)=nx^(n-1)`

`-2+6(dy)/(dx)=0`

`6(dy)/(dx)=2`

`m_2=(dy)/(dx)=(2)/(6)=(1)/(3)`

`m_2=-(1)/(m_1)=-(1)/(-3)=(1)/(3)`

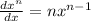
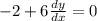
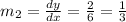
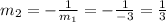
When two lines are perpendicular then ,

`m_1=-(1)/(m_2)`

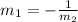
When two lines are parallel then, slope of two lines are equal.

We have

`m_2=-(1)/(m_1)=(1)/(3)`

Hence, the lines are perpendicular.