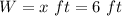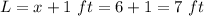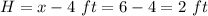Answer:
The dimensions of the box are
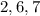
Explanation:
we know that
The volume of a box in the shape of a cube is equal to
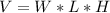
where
W is the width of the box
L is the length of the box
H is the height of the box
In this problem we have
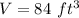
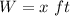
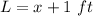
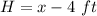
Substitute the values in the formula of volume
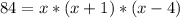
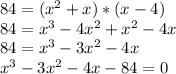
Using a graphing tool
Solve the cubic function
see the attached figure
The value of x is equal to
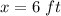
the dimensions of the box are