Question

A veterinary researcher takes an SRS of 60 horses presenting with colic. The average age of the 60 horses with colic is 12 years. The average age of horses seen at the veterinary clinic was determined to be 10 years. The researcher also determined that the standard deviation of horses coming to the veterinary clinic is 8 years. The probability that a sample mean is 12 or larger for a sample from the horse population is:

A. 0.0100.
B. 0.1264.
C. 0.0264.
D. 0.9736.

Answer 1

C. hope this helps :)

Answer 2

Answer: C. 0.0264.

Explanation:

Given : Sample size :
`n=60`

Population mean :
`\mu=10`

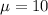
Standard deviation:
`\sigma= 8`

Sample mean :
`\overline{x}=12`

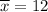
We assume that the age of horses are normally distributed.

Test statistic:

z-score :
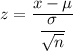
`z=\frac{\overlien{x}-\mu}{(\sigma)/(√(n))}`

i.e.
`z=(12-10)/((8)/(√(60)))\approx1.94`

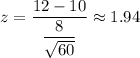
Using the standard normal distribution table , the probability that a sample mean is 12 or larger for a sample from the horse population :-

`P(x\geq12)=1-P(x<12)=1-0.9735661=0.0264339\approx0.0264`

Hence, the required probability = 0.0264