Question

Which of the following describes the function x4 − 3?

Select one:
a. The degree of the function is even, so the ends of the graph continue in opposite directions. Because the leading coefficient is positive, the left side of the graph continues down the coordinate plane and the right side continues upward.
b. The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is negative, the left side of the graph continues down the coordinate plane and the right side also continues downward.
c. The degree of the function is even, so the ends of the graph continue in opposite directions. Because the leading coefficient is negative, the left side of the graph continues up the coordinate plane and the right side continues downward.
d. The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is positive, the left side of the graph continues up the coordinate plane and the right side also continues upward.

Answer 1

The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is positive, the left side of the graph continues up the coordinate plane and the right side also continues upward.

Explanation:

The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is positive, the left side of the graph continues up the coordinate plane and the right side also continues upward.

Answer 2

Option D

Explanation:

We have given that function:
`f(x)=x^4-3`

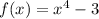
We can see this through graph attached that the coordinate of planes on the left and right moves upward.

By the definition of degree of the polynomial state that highest degree of x is the degree of polynomial i.e. 4 which is even which implies that the degree of the function is even.

The above statement implies that the degree of the function is even, so the ends of the graph continue in the same direction. As the leading coefficient is positive, the left side of the graph continues up the coordinate plane and the right side also continues upward.

therefore, option D is correct