Question

Find the slope of the normal line to y=x+cos(xy) at (0,1)

Answer 1

Derivating the equation:


`y=x+\cos(xy)\Longrightarrow y'=1+(-y\sin(xy)-xy'\sin(xy))\iff \\\\y'=1-y\sin(xy)-xy'\sin(xy)\iff y'+xy'\sin(xy)=1-y\sin(xy)\iff \\\\y'=(1-y\sin(xy))/(1+x\sin(xy))`

So the slope of the tangent in the point (0,1) is:


`y'=(1-y\sin(xy))/(1+x\sin(xy))\Longrightarrow y'=(1-1\sin(0\cdot1))/(1+0\sin(0\cdot1))\Longrightarrow y'=1`

Then, the slope of the normal (n) line in the point (0,1) is:


`n\cdot y'=-1\Longrightarrow n\cdot1=-1\iff\boxed{n=-1}`

Answer 2

Answer with explanation:

The equation of the curve is:

y= x + Cos ( x y)

Differentiating once to get,slope of tangent

y'=1 + Sin (x y)(y + x y')

Now, slope of tangent of the curve,at (0,1) can be obtained by,substituting,x=0 and y=1 , in the equation of the slope of tangent to the curve

`y'_((0,1))=1 + Sin (0 * 1)(1+0 * y'_((0,1)))\\\\ \text{as},Sin 0^(\circ)=0\\\\y'_((0,1))=1`

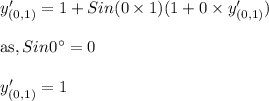
Slope of tangent = 1

For, any curve,the two lines passing through , (0,1),that is normal line and tangent line will be perpendicular to each other,so as their slopes.

So,if two lines are perpendicular to each other

Product of their Slopes = -1

So, →Slope of tangent × Slope of Normal = -1

→ 1 ×Slope of Normal=-1

→Slope of Normal= -1

Equation of line passing through, (0,1) and having slope=-1,that is equation of normal line is

→y-1= -1×(x-0)

→ y-1=-x

→ x + y-1=0→→→Equation of normal line

Slope of normal line = -1