Question

Which of the sets of ordered pairs represents a function?

A = {(1, −5), (8, −5), (8, 7), (2, 9)}
B = {(7, −4), (7, −2), (6, −3), (−9, 5)}

Only A
Only B
Both A and B
Neither A nor B

Answer 1

The answer is D, "Neither A or B."

Explanation:

In most cases (including this one), there can only be one input or x-value for every unique output, or y-value. In other words, the x-values cannot repeat themselves. Both (8, -5) and (8, 7) are invalid in ordered pairs A, and (7, -4), and (7, -2) make ordered pairs B unable to represent a function. I also took this test and it was correct.

Answer 2

The correct option is 4. Neither A nor B represents a function.

Explanation:

The given sets of ordered pairs are

`A=\{(1,-5), (8,-5), (8,7), (2,9)\}`

`B=\{(7,-4), (7,-2), (6,-3), (-9,5)\}`

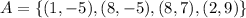
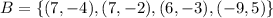
A set of ordered pairs represents a function if there exist unique outputs for all inputs. It means for each values of x there exist, a unique value of y.

In set A the value of y-coordinates are -5 and 7 at
`x=8`.

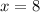At x=8, there exist more than one value of y, so the set A is not a function.

In set B the value of y-coordinates are -4 and -2 at
`x=7`.

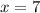At x=7, there exist more than one value of y, so the set B is not a function.

Therefore neither A nor B represents a function and option 4 is correct.