Question

What is the simplified form of the quantity 4 z squared minus 4z minus 15 over the quantity 2 z squared plus z minus 15? (6 points)

Answer 1

First you simplify it down to (2z+3)(2z-5)/(2z-5)(z+3)
Both of the brackets containing (2z-5) can now be cancelled out leaving you with a final answer of (2z+3)/(z+3)

Answer 2

Answer: The simplified form of the given equation is
`(2z+3)/(z+3)`

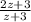
Explanation:

From the given information, the numerator of the given fraction is:
`4z^2-4z-15`

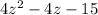
and denominator of the given fraction is
`2z^2+z-15`

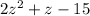
The fraction becomes:

`(4z^2-4z-15)/(2z^2+z-15)`

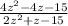
Applying middle term factorization in the numerator and denominator term, we get:

=
`(4z^2-10z+6z-15)/(2z^2+6z-5z-15)`

=
`(2z(2z-5)+3(2z-5))/(2z(z+3)-5(z+3))`

=
`((2z+3)(2z-5))/((2z-5)(z+3))`

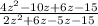
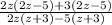
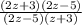
Cancelling (2z-5) factor from numerator an denominator, we get:

=
`(2z+3)/(z+3)`

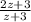
The above fraction is the simplified form of the equation formed in the question.