Question

Solve open parentheses square root of 7 close parentheses to the 6 x power = 49x−6.

x = negative 21 over 2
x = −6
x = negative 6 over 5
x = −12

Answer 1

The equation is not setup properly, possibly it is your teacher's fault.

From external research, I would say the answer is x = -12.

Answer 2

Option D is correct.

x = -12

Explanation:

Solve:
`(√(7))^(6x) = 49^(x-6)`

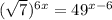
We can write 49 as:

`49 = 7 \cdot 7 = 7^2`

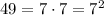
using exponent rules:

`\sqrt[n]{a^m}=a^{(m)/(n)}`

`(a^m)^n = a^(mn)`

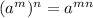
Apply this rules on the given equation:

`((7)^{(1)/(2)})^(6x) = (7^2)^(x-6)`

`7^{(6x)/(2)} = 7^(2(x-6))`

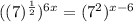
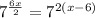
Simplify:

`7^(3x) =7^(2x-12)`

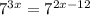
On comparing both sides we get;

`3x = 2x-12`

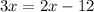
Subtract 2x from both sides we get;

x = -12

Therefore, the value of x is -12