Question

If a₀ , a₁ , a₂ , a₃ , are all positive , then 4a₀x³ + 3a₁x² + 2a₂x + a₃ = 0 has at least one root in (-1,0) if

A: a₀ + a₂ = a₁ + a₃ and 4a₀ + 2a₂ > 3a₁ + a₃
B: 4a₀ + 2a₂ < 3a₁ + a₃
C: a₀ + a₂ > a₁ + a₃ and 4a₀ + 2a₂ = 3a₁ + a₃
D: a₀ + a₂ > a₁ + a₃ and 4a₀ + 2a₂ < 3a₁ + a₃

Answer 1

If
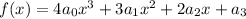
`f(x)=4a_0x^3+3a_1x^2+2a_2x+a_3`, then you have


`f(-1)=-4a_0+3a_1-2a_2+a_3`

`f(0)=a_3`

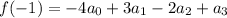
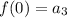
By the intermediate value theorem, there will be some number
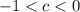
`-1<c<0` such that
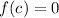
`f(c)=0` (i.e.
`f(x)` will have a root in
`(-1,0)`) if you can guarantee that
`f(-1)<f(c)<f(0)` or
`f(-1)>f(c)>f(0)`.

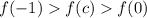
Since the coefficients
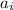
`a_i` are all positive, then you know right away that
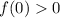
`f(0)>0`, so you need to have
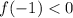
`f(-1)<0` in order for there to be such a
`c`.

This means you need to have


`-4a_0+3a_1-2a_2+a_3<0\implies 4a_0+2a_2>3a_1+a_3`

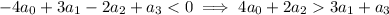
which means (A) must be the answer.