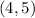Question

Find the circumcenter of triangle EFG with E(2, 6) F(2,4) and G)6,4

Answer 1

(4,5) you draw lines perpendicularly through each side and the point where they meet is the answer

Answer 2

The circumcenter is the point
`(4,5)`

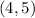
Explanation:

we know that

The circumcenter is the point where the perpendicular bisectors of a triangle intersect

so

In this problem we have

The coordinates of triangle EFG are

`E(2,6), F(2,4),G(6,4)`

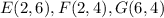
Step 1

Find the slope of the side EF

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

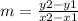
we have

`E(2,6), F(2,4)`

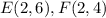
Substitute the values

`m=(4-6)/(2-2)`

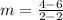
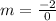`m=(-2)/(0)` -------> the slope is undefined

The side EF is parallel to the y-axis

therefore

The segment perpendicular to the side EF will be parallel to the x-axis

and the equation of the perpendicular bisector to the side EF is equal to the y-coordinate of the midpoint EF

Step 2

Find the y-coordinate of the Midpoint EF

The formula to calculate the y-coordinate of the midpoint between two points is equal to

`y=(y1+y2)/(2)`

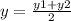
we have

`E(2,6), F(2,4)`

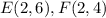
substitute the values

`y=(6+4)/(2)=5`

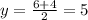
therefore

the equation of the perpendicular bisector to the side EF is equal to

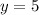`y=5` -------> equation A

Step 3

Find the slope of the side FG

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

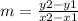
we have

`F(2,4),G(6,4)`

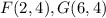
Substitute the values

`m=(4-4)/(6-2)`

`m=(0)/(4)=0`

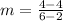
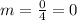
The side FG is parallel to the x-axis

therefore

The segment perpendicular to the side FG will be parallel to the y-axis

and the equation of the perpendicular bisector to the side FG is equal to the x-coordinate of the midpoint FG

Step 4

Find the x-coordinate of the Midpoint FG

The formula to calculate the x-coordinate of the midpoint between two points is equal to

`x=(x1+x2)/(2)`

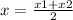
we have

`F(2,4),G(6,4)`

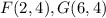
substitute the values

`x=(2+6)/(2)=4`

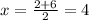
therefore

the equation of the perpendicular bisector to the side FG is equal to

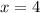`x=4` -------> equation B

Step 5

Find the intersection point equation A and equation B

we know that

the intersection point of the perpendicular bisector to the side EF and the perpendicular bisector to the side FG is called the circumcenter

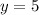`y=5` -------> equation A

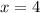`x=4` -------> equation B

The solution is the point
`(4,5)`