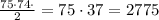Answer:
2775 ways
Explanation:
We have been given the case to choose exactly two tails when flipped 75 times means
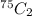
Since,
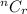 is equal to
is equal to
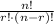
Here n =75, r=2 substituting the values we will get
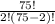
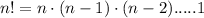
After simplification we will get
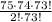
Cancel out the common term that is 73! we will get
after more simplification we will get
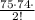
Finally, we will get