Question

Classify ABC by its sides. Then determine whether it is a right triangle.

A(3, 3), B (6, 9), C (
6,-3)

Answer 1

∴Given Δ ABC is not a right-angle triangle

a= AB = √45 = 3√5

b = BC = 12

c = AC = √45 = 3√5

Explanation:

Given vertices are A(3,3) and B(6,9)

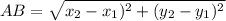
`AB = \sqrt{x_(2)-x_(1) )^(2) +(y_(2)-y_(1) )^(2) }`

AB =
`\sqrt{(9-3)^(2)+(6-3)^(2) } = \sqrt{6^(2)+3^(2) } =√(45)`

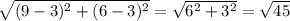
Given vertices are B(6,9) and C( 6,-3)

`B C = \sqrt{x_(2)-x_(1) )^(2) +(y_(2)-y_(1) )^(2) }`

=
`\sqrt{(-3-9)^(2)+(6-6)^(2) } =\sqrt{12^(2) } = 12`

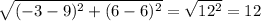
BC = 12

Given vertices are A(3,3) and C( 6,-3)

`AC = \sqrt{(6-3)^(2)+(-3-3)^(2) } = √(9+36) = √(45)`

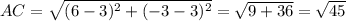
AC² = AB²+BC²

45 = 45+144

45 ≠ 189

∴Given Δ ABC is not a right angle triangle