Question

Provide the reasons for the fol owing proof

Given: JK ≅ KL, NK ≅ KM
Prove ΔNKJ ≅ ΔMLK

Statements Reasons

1. JK≅KL,NK≅KM 1. Given

2.
3. ΔNKJ ≅ ΔMLK 3.________


ANSWER CHOICES

a. reflexive property of ≅ ; SAS
b. reflexive property of ≅ ; ASA
c. vertical angles are congruent; ASA
d. vertical angles are congruent; SAS

Answer 1

Answer would be D, as the triangles are congruent due to being verticle angles (literally, you can just see theyre the same). Its SAS because you have 2 exact same sides, plus an exact same angle

Answer 2

Option d is correct.

Vertical angles are congruent;

SAS

Explanation:

Given:
`JK \cong KL` ,
`NK \cong KM`

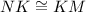
In ΔNKJ and ΔMLK

`JK \cong KL` and [Side] {Given}

`NK \cong KM`

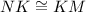
Vertical angles states that the two lines intersect to make an X, angles on opposite sides of the X are called vertical angles.

i.e
`\angle NKJ` and
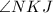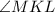`\angle MKL` are vertical angles.

Also, vertical angles are congruent.

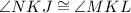`\angle NKJ \cong \angle MKL` [Angle] [Vertical angles are congruent]

SAS(Side-Angle-Side) postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

then, by SAS postulates;

`\triangle NKJ \cong \triangle MLK` Hence proved!

Therefore:

Statement Reason

1.
`JK \cong KL`,
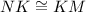`NK \cong KM` Given

2.
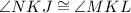`\angle NKJ \cong \angle MKL` Vertical angles are congruent

3.
`\triangle NKJ \cong \triangle MLK` SAS