Question

Which correctly describes how the graph of the inequality 5x + 2y ≥ 13 is shaded? (1 point) Above the solid line Below the solid line Above the dashed line Below the dashed line

Answer 1

The answer is above the solid line.
Tip: On problems like these, go to the website, desmos.com, press the big red button that says "Start Graphing", and you can graph any equation by typing it in on the side and it show you the graph to get the answer!

Answer 2

The graph of inequality
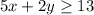`5x+2y\geq 13` is above the solid line.

Explanation:

Explanation:

An inequality on a coordinate plane consist of a boundary line and an area in which each point is a possible solution.

* If the inequality has a sign or , then the line will be a solid line and its point are included in the solution.

* If the inequality has a sign '>' or '<' , then the line will be a dotted line and its point are not included in the solution.

Given: The linear inequality:
`5x+2y\geq 13`

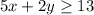
Then, the equation of the boundary line is; 5x+2y =13 ......[1]

we can write this as;

`2y = -5x+13`

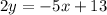
Divide by 2 we get;

`y = -(5)/(2) x + (13)/(2)` ......[2]

Compare this boundary line equation with the general point slope intercept line i.e, y = mx+b where m is the slope and b is the y-intercept.

Therefore, the slope of the this line is, m =
`-(5)/(2)`

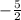
and a y-intercept (b) =
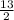`(13)/(2)` = 6.5

To find x -intercept:

Substitute y =0 in to solve for x;

`5x+0 =13`

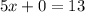
Simplify:

`x =(13)/(5) = 2.6`

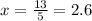
Therefore, the x-intercept is 2.6

Now,

Plot
`y = -(5)/(2) x + (13)/(2)` ( as a solid line because
`y\geq` included equal to)

and shade the area above as
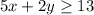`5x+2y\geq 13` as shown below in the graph