Question

A helicopter hovers 40 ft above the ground. Then the helicopter climbs at a rate of 21 ft/s. Write a rule that represents the helicopter’s height h above the ground as a function of time t. What is the helicopter’s height after 45 s?

Answer 1

starts at 40
each second climbs 21 ft
40+21(number of second)

h=40+21t
at t=45
h=40+21(45)
h=40+945
h=985

height is 985
rule is h=21t+40 or h=40+21t

Answer 2

The initial height of the helicopter is 40 ft.

For every second (let's call time as t) he climbs upward, he goes 21 ft.

So we can write height of helicopter as
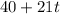`40+21t` with respect to t.

In functional notation we can write the height (f(t)) of the helicopter at time (t) as:

`f(t)=40+21t`

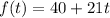
To find the height of the helicopter after 45 seconds, we plug in 45 into the equation in place of t to get:

`f(t)=40+21(45)=985`

So after 45 seconds, the height of the helicopter is 985 ft.

ANSWER:

• Equation modelling height of helicopter with respect to time:
  `f(t)=40+21t`
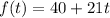
• Height of helicopter after 45 seconds is 985 ft.