You can think of simple interest as fixed - the amount of interest you earn is dependent only on the principal amount.
For example, if you took out a loan for $100 with a simple interest rate of 10% every year, your loan would increase by $10 of interest each year.
Compound interest, on the other hand, is not fixed. Best to explain by example.
Suppose that, for the $100 loan, there is a compound interest rate of 10% that is taken into account every 6 months. This means that after the first 6 months in the first year, you will have accrued $10 in interest, and so you now owe $110.
At the end of the next 6 months, the amount of interest you accrue depends on the amount you owe after the first 6 months. In other words, the 10% interest rate is now applied to the $110 balance, so the second half of the year adds 10% of $110, or $11, to the balance. At the end of the first year, then, you end up owing $121.
The number of compounding periods determines how often this recalculation of interest occurs throughout the year. The example above uses a semiannual rate (2 per year).
Let's see what happens when interest is compounded 6 times as often, i.e. each month, or 12 times a year.

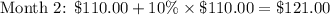
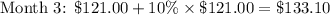
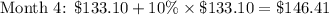



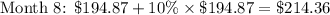
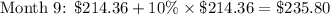
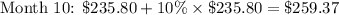

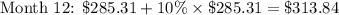
You'll notice that you end up owing over 3 times as much as what you first took on loan.
There's nothing stopping the creditor (mathematically, not necessarily legally) from setting up an arbitrary compounding rate. For instance, if interest is compounded daily, you could theoretically end up owing
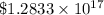
- about $128 quadrillion by the end of the year!