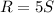Answer:
Table N

Explanation:
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
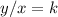 or
or
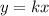
In this problem the table N
 represent a proportional relationship
represent a proportional relationship
Find the value of k
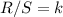
For
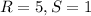
substitute
tex]k=5/1=5[/tex]
For
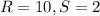
substitute
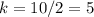
For
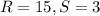
substitute
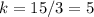
For
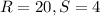
substitute
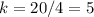
For
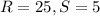
substitute
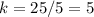
the equation of the proportional relationship is equal to