Question

A series contains 18 numbers and has a sum of 4,185. The last number of the series is 275. What is the first number?

Answer 1

B) 190

Explanation:

a1 = 190

Answer 2

I'll assume the sequence is arithmetic just because that would involve less work (and in fact, if the series is geometric, there is more than one solution).

So the sequence takes the form
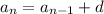
`a_n=a_(n-1)+d`, where
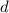
`d` is the common difference between successive terms. You can solve this recursively to find an explicit solution for
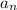
`a_n` in terms of the first term in the sequence, namely


`a_n=a_1+(n-1)d`

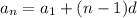
Now, the summation of the first
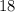
`18` terms of the sequence amounts to


`\displaystyle\sum_(n=1)^(18)a_n=\sum_(n=1)^(18)(a_1+(n-1)d)=18a_1-18d+d\sum_(n=1)^(18)n`

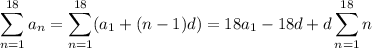
The last sum can be computed using the formula


`\displaystyle\sum_(k=1)^nk=\frac{n(n+1)}2`

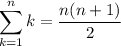
so you end up with


`4185=\displaystyle\sum_(n=1)^(18)a_n=18a_1-18d+\frac{18*19}2d=18(a_1-d)+171d`

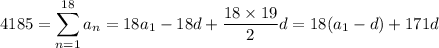
Meanwhile, you know the last term in the series is
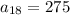
`a_(18)=275`, so you end up with another equation


`a_(18)=a_1+(18-1)d\implies 275=a_1+17d`

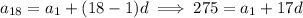
You have enough information to solve for
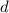
`d` and, more importantly,
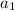
`a_1`. You should get
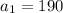
`a_1=190` (and the common difference turns out to be
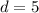
`d=5`).