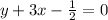Question

Given triangle GHI with G(4.-3), H(-4,2), and I(2,4), find the perpendicular bisector of line HI in standard form.

Answer 1

Hope it helped you.

Answer 2

`y+3x-(1)/(2)=0`

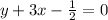
Explanation:

The perpendicular bisector is basically the line that intercept the side HI in its midpoint with a right angle. To find the equation of such line, we first have to find the slope of side HI, which coordinates are H(-4,2) and I(2,4)

`m_(HI)=(4-2)/(2-(-4))=(2)/(6)=(1)/(3)`

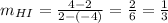
Now, the condition of perpendicularity is

`m_(HI)m_(\perp)=-1`

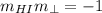
We replace the slope of HI to find the slope of the perpendicular bisector

`m_(HI)m_(\perp)=-1\\(1)/(3)m_(\perp) =-1\\m_(\perp) =-3`

We already have the slope of the perpendicular bisector, now we just a points that this line crosses. We know that a perpendicular bisector intercept the midpoint, so we have to find the midpoint of HI

`M((4+(-4))/(2) ,(-3+2)/(2) )\\M((0)/(2),(-1)/(2))\\M (0,-(1)/(2))`

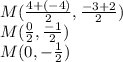
Now we know the point we use the point-slope from to find the equation

`y-y_(1) =m(x-x_(1))\\y-(1)/(2)=-3(x-0) \\y=-3x+(1)/(2)`

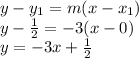
Therefore, the standard form of the perpendicular bisector of line HI is

`y+3x-(1)/(2)=0`