Question

If the population of a country increases at a rate of 1.5% annually, and its current population is 430,000, how many years will it take for the population to triple?

Answer 1

3p=p(1+0.015)^n
3=(1.015)^n
n=Log(3)/log(1.015)
n=??

Answer 2

Hence, it will take about 73 years for the population to triple.

Explanation:

For this case we have an exponential function P(t) which represents the population at time 't' ; which is given as:

i.e. the equation is represented of the form:

`P(t)=Ab^t`

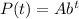
Where,

A: initial amount ( Here we have A=430000)

b: growth rate (Here we have b=1.015)

t: time in years.

As the population has to triple over the time.

Hence, Substituting values we have:

`3* 430000=430000* (1.015)^t`

⇒
`3=(1.015)^t`

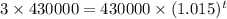
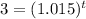
Taking logarithmic function on both side we have:

`\log3=t\log1.015`

( Since
`\log m^n=n \log m` )

⇒
`t=(\log 3)/(\log 1.015)\\\\t=73.78876233`

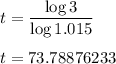
Hence, It will take for the population to triple about:

t = 73 years