Answer:
The equation which can be solved by inverse property is:
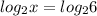 .
.
Explanation:
The inverse property of Logarithms:
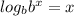
or
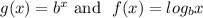
From the provided option
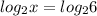 can be solved using the inverse property.
can be solved using the inverse property.
Consider the option 1.
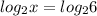
Use the inverse property of logarithms:
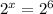
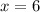
Thus,
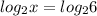 can be solved by inverse property.
can be solved by inverse property.