Question

The number of books borrowed from a library each week follows a normal distribution. When a sample is taken for several weeks, the mean is found to be 190 and the standard deviation is 30. There is a ___% chance that more than 250 books were borrowed in a week.

Answer 1

`\mathbb P(X>250)=\mathbb P\left((X-190)/(30)>(250-190)/(30)\right)=\mathbb P(Z>2)\approx0.0228`

Or, if you're familiar with the empirical rule and the basic properties of the normal distribution, you can use the fact that approximately
`95/%` of the distribution lies within two standard deviations of the mean, or


`\mathbb P(|Z|<2)=\mathbb P(-2<Z<2)\approx 0.95`

which means about
`5\%` of the distribution lies outside this interval, or


`\mathbb P((-2<Z)\cup(Z>2))\approx0.05`

Because the distribution is symmetric, you have


`\mathbb P(-2<Z)=\mathbb P(Z>2)`

`\implies \mathbb P((-2<Z)\cup(Z>2))=\mathbb P(-2<Z)+\mathbb P(Z>2)=2\mathbb P(Z>2)\approx0.05`

`\implies \mathbb P(Z>2)\approx 0.025`

Answer 2

There is a 2.28% chance that more than 250 books were borrowed in a week.

Explanation:

Given : The number of books borrowed from a library each week follows a normal distribution. When a sample is taken for several weeks, the mean is found to be 190 and the standard deviation is 30.

To find : There is a ___% chance that more than 250 books were borrowed in a week ?

Solution :

Formula to find z-score is

`z=(x-\mu)/(\sigma)`

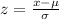
Where,
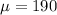`\mu=190` is the mean

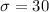`\sigma=30` is the standard deviation

x=250 is the value

Substitute the value in the formula,

`z=(250-190)/(30)`

`z=(60)/(30)`

`z=2`

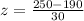
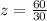
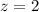
According to the normal distribution table, P(z<2) = 0.9772

Now, The probability that more than 250 books were borrowed in a week will be

`P(x>250)=P(z>2)= 1-P(z<2) =1-0.9772=0.0228 = 2.28\%`

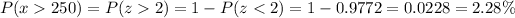
Therefore, There is a 2.28% chance that more than 250 books were borrowed in a week.