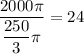Question

he radius of the base of a cylinder is 10 centimeters, and its height is 20 centimeters. A cone is used to fill the cylinder with water. The radius of the cone's base is 5 centimeters, and its height is 10 centimeters. The number of times one needs to use the completely filled cone to completely fill the cylinder with water is?

Answer 1

Volume of cylinder:
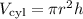
`V_{\text{cyl}}=\pi r^2h`, where
`r` is the radius and
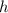
`h` is the height. This volume is
`\pi*10^2*20=2000\pi` (cubic cm).

Volume of cone:
`V_{\text{cone}}=\frac13\pi r^2h`, with the same variables denoting the same parameters. This volume is
`\frac13\pi*5^2*10=\frac{250}3\pi` (also cubic cm).

The number of times it would take to fill the cylinder with water using the cone as a source would be


`\frac{2000\pi}{\frac{250}3\pi}=24`