You can complete the square to find the equation of the circle in standard form.
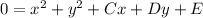
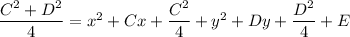
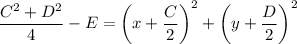
So the circle is centered at
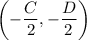
and has radius
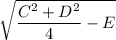
.
A horizontal shift to the left can be done by adding a positive number to the

term, as in
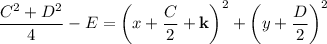
Expanding, you end up with
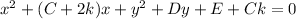
So the coefficient
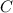
is increased by twice the horizontal shift, while
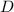
remains unchanged.