Question

Solve For X

please help, thank you :}

Answer 1

Given:

Two secants intersecting each other outside the side the circle.

To find:

The value of x.

Solution:

Using Intersecting Secant Theorem, we get

`x(x+8)=4(4+8)`

`x^2+8x=4(12)`

`x^2+8x=48`

`x^2+8x-48=0`

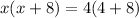
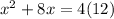
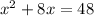
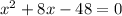
Using splitting the middle terms, we get

`x^2+12x-4x-48=0`

`x(x+12)-4(x+12)=0`

`(x+12)(x-4)=0`

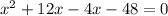
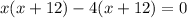
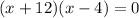
Using zero product property, we get

`(x+12)=0\text{ and }(x-4)=0`

`x=-12\text{ and }x=4`

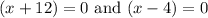
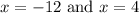
Side length cannot be negative, i.e.,
`x\\eq -12`.

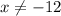Therefore, the only value of x is 4.