Question

How do I find the critical points?


`( x^(2) - 1)^3`

Intervals: [ -1, 2]

Answer 1

Critical points is where the derivative (slope) is zero or does not exist. So to do this we have to find the derivative of our function:


`(d)/(dx)(x^(2) - 1)^(3)`

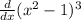
So we apply chain rule:

=
`3(x^(2) - 1)^(2) * 2x`

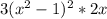
Set our first derivative to zero and solve for x:

3(x^2 - 1) * 2x = 0

So we can see that (by plugging in) 0, -1 and 1 makes our solution true

So our critical value is x = 0, x = -1, x = 1