Question

Write (9 + 6i) − (1 + 3i) as a complex number in standard form.

A)10 + 9i
B)8 − 3i
C)8 + 3i
D)7 − 12i

Answer 1

a + bi is the standard form of a complex number.
You would treat complex numbers just like any other numbers a far as adding and subtracting like terms.
9 + 6i - 1 - 3i = 8 + 3i Letter C is the answer

Answer 2

option (c) is correct.

(9 + 6i) − (1 + 3i) in standard form is 8+3i

Explanation:

Given : (9 + 6i) − (1 + 3i)

We have to write the given complex number in standard simplified form.

Consider the given complex number (9 + 6i) − (1 + 3i)

Grouping the real part and the imaginary parts

`\left(a+bi\right)\pm \left(c+di\right)=\left(a\:\pm \:c\right)+\left(b\:\pm \:d\right)i`

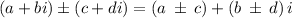
We get,

`=\left(9-1\right)+\left(6-3\right)i`

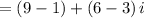
On simplifying , we get,

`=8+3i`

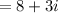
Thus, option (c) is correct.