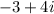
is a complex number that satisfies
![\begin{cases}r\cos x=-3\\[1ex]r\sin x=4\\[1ex]r=√((-3)^2+4^2)\end{cases}](https://img.qammunity.org/2018/formulas/mathematics/high-school/bf81dhyghp4v9ik1p2uta1t8xmh7lbt8mu.png)
The last equation immediately tells you that
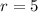
.
So you have
![\begin{cases}\cos x=-\frac35\\[1ex]\sin x=\frac45\end{cases}](https://img.qammunity.org/2018/formulas/mathematics/high-school/1tk13yib1trsxpxy8qpiq38xtfd42sqyz1.png)
Dividing the second equation by the first, you end up with

Because the argument's cosine is negative and its sine is positive, you know that
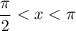
. This is important to know because it's only the case that

whenever

. The inverse doesn't exist otherwise.
However, you can restrict the domain of the tangent function so that an inverse can be defined. By shifting the argument of tangent by

, we have
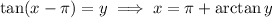
All this to say
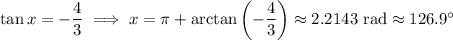
So,
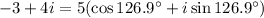
.