Question

8 A small smooth object slides from rest down a smooth inclined plane inclined at

30° to the horizontal. What is (i) the acceleration down the plane, (ii) the time
to reach the bottom if the plane is 5 m long?
The object is now thrown up the plane with an initial velocity of 15 ms -1.
(iii) How long does the object take to come to rest? (iv) How far up the plane has
the object then travelled?​

Answer 1

(i) The acceleration of the object down the plane is approximately 4.9 m/s²

(ii) The time it takes for the object to reach the bottom is approximately
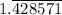`1.\overline{428571}` seconds

(iii) The time it takes the object to come to rest is approximately 1.030636 seconds

(iv) The object has travelled past the top of the plane by time it comes to rest

Step-by-step explanation:

(i) The given parameter for the objects motion are;

The angle of inclination of the plane with the horizontal, θ = 30°

The length of the plane, s = 5 m

Let "a" represent the acceleration down an inclined plane, due to the acceleration under gravity "g" we have;

a = g × sin(θ)

Where;

g = The acceleration due to gravity ≈ 9.8 m/s²

∴ a ≈ 9.8 m/s² × sin(30°) = 9.8 m/s² × 0.5 = 4.9 m/s²

The acceleration of the object down the plane, a ≈ 4.9 m/s²

(ii) The time it takes for the object to reach the bottom, can be found from the following kinematic equation of motion;

s = u·t + 1/2·a·t²

Where;

s = The length of the inclined plane = 5 m

u = The initial velocity of the object = 0 m/s

t = The time of motion of the object (Here the time to reach the bottom of the plane)

a = The acceleration of the object = 4.9 m/s²

Therefore, we have;

5 = 0 × t + 1/2 × 4.9 × t² = 2.45·t²

t² = 5/2.45 = 100/49

t = √(100/49) = 10/7 =
`1.\overline{428571}`

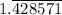
The time to reach the bottom of the plane = t =
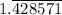`1.\overline{428571}` seconds

(iii) When the object is thrown up the plane with an initial velocity of 15 m/s, the time, "t", it takes the object to come to rest is found by the following kinematic equation of motion;

v² = u² - 2·a·s

Therefore, we have;

v² = 15² - 2 × 4.9 × 5 = 176

v = √176 = 4·√11

The velocity of the object at the top of the plane = v = 4·√11 m/s

The time it takes the object to come to rest after reaching the top of the plane = The time it takes the object (projectile) to reach maximum height

`t_m = (v_i \cdot sin(\theta _i ))/(g)`

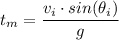
Where;

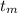`t_m` = The time it takes the object to reach maximum height

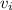`v_i` = The initial velocity of the object at the top of the inclined plane = 4·√11 m/s

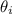`\theta _i` = The initial angle of inclination of the path of the object with the horizontal = 30°

Therefore, we have;

`t_m = (4 * √(11) * sin(30^(\circ) ))/(9.8) = (10 \cdot √(11) )/(49) \approx 0.67686`

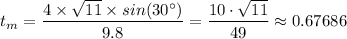
The time it takes the object to come to rest after reaching the top of the plane = The time it takes the object to reach maximum height =
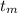`t_m` ≈ 0.67686 seconds

The time it takes the object to reach the top of the plane,
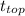`t_(top)`, is given from the kinematic equation of motion, v = u - a·t, as follows

v = u - a·t

∴ t = (u - v)/a

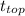`t_(top)` = (15 - 4·√11)/4.9 ≈ 0.353776

The time it takes the object to reach the top of the plane =
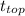`t_(top)` ≈ 0.353776 s

The total time it takes the object to come to rest, ∑t =
`t_m` +
`t_(top)`

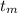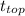
∴ ∑t ≈ 0.67686 + 0.353776 = 1.030636

The time it takes the object to come to rest = ∑t ≈ 1.030636 seconds

(iv) The distance up the plane the object reaches, "s", is given by the following kinematic equation;

s = u·t - 1/2·a·t²

Therefore, we have;

s = 15 × 15/4.9 - 1/2 × 4.9 × (15/4.9)² ≈ 22.959 m

However, the plane is 5 meters long, therefore, the object goes further than the top of the plane.