Question

8x^3+2x^2-8 estimate the relative maxima and relative minima

Answer 1

Compute the derivative:


`(\mathrm d)/(\mathrm dx)\bigg[8x^3+2x^2-8\bigg]=24x^2+4x`

Set equal to zero and find the critical points:


`24x^2+4x=4x(6x+1)=0\implies x=0,-\frac16`

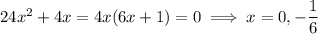
Compute the second derivative at the critical points to determine concavity. If the second derivative is positive, the function is concave upward at that point, so the function attains a minimum at the critical point. If negative, the critical point is the site of a maximum.


`(\mathrm d^2)/(\mathrm dx^2)\bigg[8x^3+2x^2-8\bigg]=(\mathrm d)/(\mathrm dx)\bigg[24x^2+4x\bigg]=48x+4`

At
`x=0`, the second derivative takes on the value of
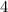
`4`, so the function is concave upward, so the function has a minimum there of
`-8`.

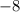
At
`x=-\frac16`, the second derivative is
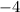
`-4`, so the function is concave downward and has a maximum there of
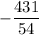
`-(431)/(54)`.