Question

Describe the translation of the graph of y = x2 that results in the graph of y = (x - 3)2.

left 3 units
right 3 units
down 3 units
up 3 units

Answer 1

Right 3 units is right out of the options given

Answer 2

Shift right by 3 units.

Second option is correct.

Explanation:

The parent function is given by
`y=x^2`

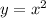
The translated function is
`y=(x-3)^2`

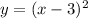
The transformation rule is:

When we subtract some constant "c" to the x values of the function f(x) then the graph will shift right by "c" units. And the transformation function would be f(x-c).

Now, here 3 is subtracted in the x value of the parent function
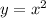`y=x^2` to get the function
`y=(x-3)^2`

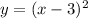
Therefore, the graph of the transformation function would shift right by 3 units.

We can see it in the attached graph as well. The vertex of the parabola
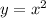`y=x^2` is at (0,0) and the vertex of the parabola
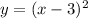`y=(x-3)^2` is at (3,0).

It means that graph has shifted 3 units to the right.

Second option is correct.