Consider as an example the function
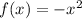
. At

and
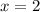
, you have

. The average rate of change of the function over the given interval is
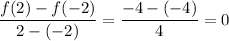
so Hunter is correct.
Maggie is also correct, since

has a turning point at the parabola's vertex when

.
For a more general situation, you can invoke Rolle's theorem, which states that for a continuous function

over an interval
![[a,b]](https://img.qammunity.org/2018/formulas/mathematics/high-school/kldvrk2yp9l3kb20ts8c2s7rinwnzb83ow.png)
with
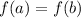
(which is the case for this example) that there is some

in the open interval
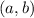
such that
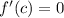
.
Whenever
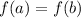
, it's always true that the average rate of change will be
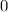
. Provided the function isn't constant, it will always attain an extremum within the given interval, so a turning point must exist.