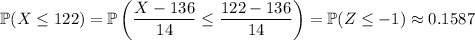
which means
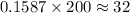
studied 122 or fewer hours.
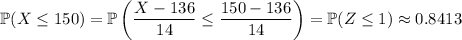
which means
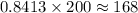
studied 150 or fewer hours.
So, neither of the first two are false.
Depending on your definition of "majority", you could also eliminate the third option. From the above calculations, you know that students that studied between 122 and 150 hours fall within 1 standard deviation of the mean, which corresponds to approximately 65% of the student population. "Majority" is often taken to mean "more than 50%", so this is also true.
This leaves us with the last option. For fun, let's compute that probability.
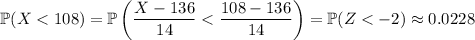
which means

students studied less than 108 hours.