First show the statement holds for the base case (presumably
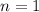
):
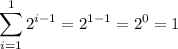
Meanwhile, the right hand side evaluates to
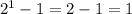
, so the base case holds.
Now assume the formula holds for
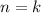
; that is,

and use this hypothesis to show that the formula holds for
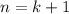
. You have
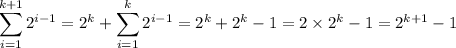
so the formula holds and the proof is complete.