Question

A person is standing on a raft; their

combined mass is 233 kg. What is the
volume of water displaced by the raft?
[?] m3
Pwater = 1,000 kg/m3

Answer 1

the volume displaced by the raft = 0.233 m3

Step-by-step explanation:

correct for Acellus

Answer 2

The volume of water displaced by the raft is 0.233 m³

Step-by-step explanation:

The question relates to Archimedes' principle which states that the buoyant force experienced by an object immersed in a fluid is equal to the weight of (the force of gravity on) the displaced fluid

The given parameters are;

The combined mass of the person and the raft, m = 233 kg

The liquid on which the raft is located = Water

The density of water,
`\rho _(water)` = 1000 kg/m³

Weight = Mass, m × g

Where;

m = The mass of the object

g = The acceleration due to gravity = 9.8 m/s²

Given that the raft is on the surface of the water (floating), the buoyant force is equal to the combined weight of the person and the raft = 233 kg

The combined weight of the person and the raft,
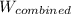`W_(combined)` = 233 kg × 9.8 m/s² = 2,283.4 N

Therefore;

The buoyant force = 2,283.4 N = The weight of the water displaced

The mass of the water displaced,
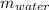`m_(water)`, = 2,283.4 N/(9.8 m/s²) = 233 kg

Density = Mass/Volume

The volume of water displaced by the raft = The mass of the water displaced/(The density of the water) = 233 kg/(1,000 kg/m³) = 0.233 m³.