Question

If the discriminant of a quadratic equation is equal to -8, which statement describes the roots?

A.) There are two complex roots.
B.) There are two real roots.
C.) There is one real root.
D.) There is one complex root.

Answer 1

There are two complex roots

Answer 2

Keywords

quadratic equation, discriminant, complex roots, real roots

we know that

The formula to calculate the roots of the quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}}{2a}`

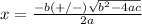
where

The discriminant of the quadratic equation is equal to

`b^(2)-4ac`

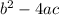
if
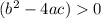`(b^(2)-4ac)> 0` ----> the quadratic equation has two real roots

if
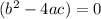`(b^(2)-4ac)=0` ----> the quadratic equation has one real root

if
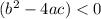`(b^(2)-4ac)< 0` ----> the quadratic equation has two complex roots

in this problem we have that

the discriminant is equal to
`-8`

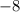
so

the quadratic equation has two complex roots

therefore

the answer is the option A

There are two complex roots