Question

Find a point on the curve y= x^2 that is closest to the point (18, 0).? Find a point on the curve y= x^2 that is closest to the point (18, 0). After taking the derivative of this one, what should I do? plug in different values into the derivative?

Answer 1

You're trying to minimize the distance between the point
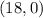
`(18,0)` and an arbitrary point on the curve,
`(x,y)=(x,x^2)`.

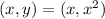
The distance between two such points is given by the function


`d(x)=√((x-18)^2+(x^2-0)^2)=√(x^4+x^2-36x+324)`

so this is the function whose derivative you should check.

But before you do that, it's helpful to know that
`d(x)` is minimized at the same point as the modified distance function
`d^*(x)=d^2(x)=x^4+x^2-36x+324`.

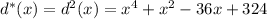
Differentiating, you have


`(\mathrm d)/(\mathrm dx)d^*(x)=4x^3+2x-36`

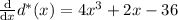
Set this to zero and solve for the critical points.


`4x^3+2x-36=2(2x^3+x-18)=0`

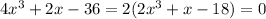
You can use the rational root theorem to find some potential candidates for roots to the cubic. The constant term has factors
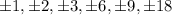
`\pm1,\pm2,\pm3,\pm6,\pm9,\pm18`, while the leading coefficient has factors
`\pm1,\pm2`. The only candidates for rational roots are
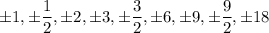
`\pm1,\pm\frac12,\pm2,\pm3,\pm\frac32,\pm6,\pm9,\pm\frac92,\pm18`. The only one of these that works is
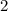
`2`, so
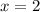
`x=2` is a root to the cubic above.

Polynomial division reveals that we can factor the cubic as


`2(x-2)(2x^2+4x+9)=0`

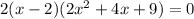
which has only one real root at
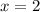
`x=2`. Checking the value of the derivative of
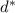
`d^*` to the left and right of this point confirms that a minimum occurs here.

Therefore the closest point on the curve to
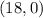
`(18,0)` is
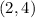
`(2,4)`.