Question

⦁ Suppose that the number of bacteria in a dish increases by 50% every four hours. there are 64 bacteria initially. write a function that describes the number of bacteria after t hours have passed. use your function to find out how many bacteria there will be after 100 hours.

Answer 1

It increases 50% every 4 hours.

Let the initial amount be N

After 4 hours, it increases by 50%, so it becomes 1.5*N
(50% increase is multiplying by a factor of 100% + 50% = 150% = 1.5)

After 4 hours again it will be multiplied by 1.5.

For the t hours, we need to know how many 4 hours are there

= (t/4)

So the increase will be: 1.5 * 1.5* 1.5*......N

The number of 1.5 will be equal to the number of 4 hours in t hours = (t/4)

Function =
`1.5^{ (t)/(4) } N`

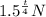
After 100 hours, t = 100, N = 64

Amount there will be =
`(1.5^{ (100)/(4) })*64`

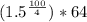
= (1.5^25) * 64

≈ 1616074.77

Hope this explains it.

Answer 2

Starting with N = N₀·(1+r)^(t/4)
where N is the number of bacteria at t hours, r is the growth rate, and N₀ is the initial number of bacteria
N₀ = 64
r = 50% = 0.5
So the formula is:
N = 64 · (1+0.5)^(t/4)
N = 64·(1.5)^(t/4)

So after 100 hours,
N = 64 · (1.5)²⁵ = 1.6×10⁶
There are 1.6×10⁶ bacteria at 100 hours.