Answer:
Option b is correct
30 is the average rate of change of f(x) over the interval [1, 5]
Explanation:
Average rate of change (A(x)) of f(x) over interval [a, b] is given by:
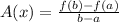 ....[1]
....[1]
As per the statement:
Given the function:
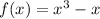
We have to find the average rate of change of f(x) over the interval [1, 5].
At x = 1
then;
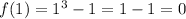
At x= 5
then;

Substitute these given values in [1] we have;
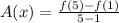
⇒
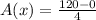
⇒
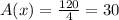
Therefore, the average rate of change of f(x) over the interval [1, 5] is, 30